[На главную] [Математика]
Математика
У моего ребенка проблемы с математикой связаны только с непониманием задачи описанной текстом. Т.е. проблема не с самой математикой, а с чтением. Поэтому никаких упражнений направленных на освоение математики мы не делали Спустя 2 года обнаружилась проблема с дробями, мы выполнили Упражнение 9, Главы 19, книги "Дар обучения". Ребенок начал решать задачки с дробями. С решением уравнений были сложности. Так же он не мог запомнить, чему равна длина окружности и площадь круга. Я написал формулы на магнитной доске, висящей в его комнате, и каждый день спрашивал его. Через 2 недели формулы врезались в его сознание, однако только в одну сторону. Вопрос: "что такое 2пR" ставил ребенка в ступор. Лепка дала лучше результат. Определитесь с проблемой. Что вызывает затруднение: не умеет считать, не понимает цифры, не понимает действия, формулы, уравнения, и работайте над проблемой самостоятельно. Разумеется книга "Дар обучения" вам в помощь. В ней Дейвис дает стратегию коррекции проблем с математикой. Примеры освоения символов и понятий.
Осваиваем числа

 Из общения с мамой ребенка-дислектика, прошедшего курс по Дейвису, выяснилось, что ребенок игнорирует числа, содержащие цифру 7, т.е. пропускает при счете 7, 17, 27, 37 и т.д. Судя по всему с цифрой 7 у ребенка связаны какие-то негативные ассоциации, которые в свою очередь являются источником дезориентации. Они справились с этой проблемой.
Из общения с мамой ребенка-дислектика, прошедшего курс по Дейвису, выяснилось, что ребенок игнорирует числа, содержащие цифру 7, т.е. пропускает при счете 7, 17, 27, 37 и т.д. Судя по всему с цифрой 7 у ребенка связаны какие-то негативные ассоциации, которые в свою очередь являются источником дезориентации. Они справились с этой проблемой.
Лепили соответствие "цифра-число-количество", считали до 10, до 20, десятками до 100, сотнями до 1000 и обратно. Играли в игры с использованием цифры 7. В конечном итоге, ребенок привык, что после 6 и перед 8 стоит 7.
Осваиваем формулы
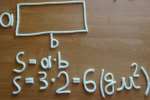 Вот пример проработки площади прямоугольника по методу Дейвиса, присланный мне. По аналогии с освоением слов. Просим ребенка "Соберись", далее он обводя свою работу пальцем говорит:
Вот пример проработки площади прямоугольника по методу Дейвиса, присланный мне. По аналогии с освоением слов. Просим ребенка "Соберись", далее он обводя свою работу пальцем говорит:
"Площадь прямоугольника S равна произведению его сторон a и b. Площадь измеряется в квадратных единицах, например: площадь прямоугольника со сторонами 2 дм. и 3 дм. равна 6 дм. квадратных"
Мысленно фотографирует свою работу. Закрываете её чистым листом и просите повторить по памяти. Затем записывает формулу в тетрадку, а вы фотографируете на телефон и записываете в дневник. Оставляете модель на виду, срок жизни до следующего занятия. Прежде чем сломать, спрашиваете, чему равна площадь прямоугольника. В случае необходимости увеличиваете срок жизни модели. Новые модели лепите на другом листе. Каждый день спрашивайте, чему равна площадь прямоугольника. Настанет такой день, когда ребенок даст ответ без запинок, после этого можете без сожаления ломать пластилиновую модель - цель достигнута.
Решаем уравнения
Мой ребенок не понимал принципы решения уравнений. Уравнение типа 2Х=6, решал зачастую так: Х=6-2. Все объяснения про перенос чисел, изменение знаков и выполняемых действий дали нулевой результат. Объяснение про "весы" тоже не дало никакого результата, более того вызвало сопротивление со стороны ребенка, поскольку расходилось с тем, что ему давали в школе. Из общения с учителем математики выяснилось, что понятие "весов" давалось в начале года и с тех пор благополучно забыто. Даже после того, как мы с ребенком слепили весы из пластилина и на их чаши положили части уравнения - результат по прежнему был нулевой. Ребенок не понимал сути.
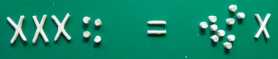 Дело сдвинулось, когда мы слепили вот это.
Дело сдвинулось, когда мы слепили вот это.
Объяснение: чтобы не нарушать равновесие нужно из обеих частей вычесть по 4 шарика, затем по одному Х, затем разделить на 2. То, что останется и есть ответ. Прошли и в обратную сторону. Положили слева Х, справа несколько шариков, затем добавили к обеим частям одинаковое количество шариков и иксов, получилось уравнение, которое решилось на ура. Процесс пошел.



 Из общения с мамой ребенка-дислектика, прошедшего курс по Дейвису, выяснилось, что ребенок игнорирует числа, содержащие цифру 7, т.е. пропускает при счете 7, 17, 27, 37 и т.д. Судя по всему с цифрой 7 у ребенка связаны какие-то негативные ассоциации, которые в свою очередь являются источником дезориентации. Они справились с этой проблемой.
Из общения с мамой ребенка-дислектика, прошедшего курс по Дейвису, выяснилось, что ребенок игнорирует числа, содержащие цифру 7, т.е. пропускает при счете 7, 17, 27, 37 и т.д. Судя по всему с цифрой 7 у ребенка связаны какие-то негативные ассоциации, которые в свою очередь являются источником дезориентации. Они справились с этой проблемой.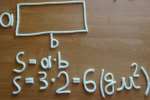 Вот пример проработки площади прямоугольника по методу Дейвиса, присланный мне. По аналогии с освоением слов. Просим ребенка "Соберись", далее он обводя свою работу пальцем говорит:
Вот пример проработки площади прямоугольника по методу Дейвиса, присланный мне. По аналогии с освоением слов. Просим ребенка "Соберись", далее он обводя свою работу пальцем говорит: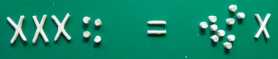 Дело сдвинулось, когда мы слепили вот это.
Дело сдвинулось, когда мы слепили вот это.
